Estamos de volta ainda com o tema mais preocupante dos últimos tempos, o COVID-19. Agora que a curva de crescimento está melhor definida, a função de Gompertz explica muito bem o comportamento da evolução do vírus, inclusive com o pico bem definido tanto para número de infectados quanto para o número de mortes.
Sei que não é um assunto agradável mas é do interesse de todos nós. Temos que continuar usando máscara, lavando as mãos com mais frequência e com o distanciamento social ainda presente em nossas vidas. Mas vai passar, assim como tudo na vida.
Abraços.
PS: Você pode conferir o artigo aqui pelo blog ou se preferir fazer o download do artigo.
Atualização da evolução do COVID-19
Autor: Edson Rui Montoro
Diariamente acompanhamos os dados de incidência e do número de mortes devido ao COVID-19 no Brasil e em algumas cidades de nosso interesse e resolvemos compartilhar os estudos sobre a situação atual do Brasil. Como já citado no nosso artigo anterior, A Matemática ajudando a prever a evolução do COVID, usamos o modelo sigmoidal de Gompertz para acompanhar a evolução dessa pandemia.
Para a atualização dos dados presentes nesse estudo, usamos como referência o site https://brasil.io/dataset/covid19/caso/.
Utilizamos o Solver do Excel® para ajustar a função de Gompertz (equação 1) sendo que essa função exponencial dupla vem apresentando um excelente ajuste, tanto para o número de infectados acumulados (R2 = 0,9997), como para o número de mortes (R2 = 1,000).

Onde y é o número de casos acumulados; k, a e b são os parâmetros da curva, sendo que k corresponde ao patamar superior da curva (assíntota), a o início da subida da curva e o b a taxa de crescimento da curva, conhecido como capacidade intrínseca de crescimento.
Hoje pretendemos atualizar os leitores com relação ao número de casos e ao número de mortes devido ao COVID-19. Os dados são do Brasil, mas sabemos que cada região está em um momento diferente, então não utilizem as conclusões aqui presentes para uma região específica.
Os dados diários acumulados (desde o dia 17/03/2020) estão representados nas Figuras 1.a e 1.b, sendo o número de casos acumulado e o número de mortes acumulado respectivamente.

Figura 1 – (a) Número de casos acumulados e (b) Número de mortes acumuladas – Brasil.
As curvas do número de casos acumulado (Figura 1.a) e o número de mortes acumuladas (Figura 1.b) apresentam o respectivo crescimento bruto e a curva de Gompertz se ajustando aos dados.
Os parâmetros da função de Gompertz são:
Para os dados de infectados: k = 7.109.415,056; a = 2,506 e b = 0,016;
Para os dados de mortes: k = 151.741,100; a = 2,028 e b = 0,020.
A primeira derivada de uma função nos fornece informações sobre um ponto de inflexão, ou como se costuma chamar, o pico; enquanto a segunda derivada produz esse ponto com muito mais clareza. Pode-se associar a primeira derivada à velocidade de propagação e a segunda derivada à sua aceleração. Assim apresentamos as derivadas da função de Gompertz, que auxiliarão para a interpretação dessa função.
As curvas da primeira derivada (equação 2) são apresentadas nas Figura 2.a (número de casos) e 2.b (número de mortes) e apresentam a respectiva taxa de crescimento.

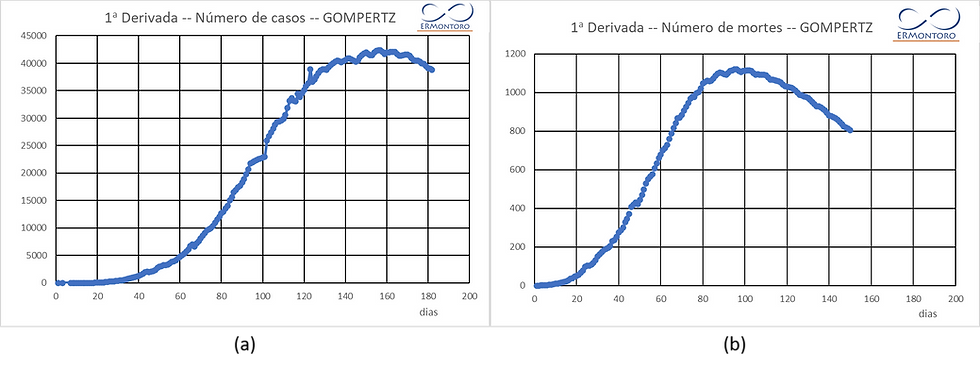
Figura 2 – Primeira derivada de Gompertz – (a) Número de casos e (b) Número de mortes
Para o número de casos (2.a), o pico da curva corresponde ao 155º dia (30/07/2020) e já desde esse dia o Brasil está em um decréscimo do número de contágios diários.
Nota-se que o pico da curva para o número de mortes (2.b) corresponde ao 102º dia (26/06/2020), desde esse dia o Brasil está em um decréscimo do número de mortes diários.
A segunda derivada, dada pela equação 3 apresenta a aceleração do número de casos e é apresentada nas Figura 3.a e 3.b.


Figura 3 – Segunda derivada de Gompertz – (a) número de casos e (b) número de mortes.
Nos gráficos da segunda derivada fica mais fácil verificar o pico, pois é quando a curva corta o eixo do zero, aproximadamente no 155º dia para o número de infectados e no 102º dia para o número de mortes, que correspondem a 30/07/20 e 26/06/20, respectivamente.
Até o dia de hoje (179º dia desde a identificação da primeira pessoa infectada e 150º dia desde a primeira morte oficial), foram 3.605.726 pessoas infectadas e 114.772 mortes no Brasil e baseado na função de Gompertz, o parâmetro k fornece o valor correspondente à parte superior da curva, baseando-se no modelo é possível estimar que teremos até o final da pandemia, aproximadamente 7.128.004 casos de infectados e chegaremos a 151.741 mortes. Assim pode-se dizer que estamos com aproximadamente 50% do número final de infectados e 70% do número total de mortes previsto, infelizmente.
Nos primeiros meses da pandemia os parâmetros mudavam todos os dias, inclusive a data prevista para o pico da pandemia. Depois de um tempo, esses parâmetros se estabilizaram, tanto como a previsão do pico, pois a curva já está razoavelmente bem definida.
Com estes parâmetros estabilizados, se torna possível fazer uma previsão para um tempo maior e com isso obtivemos as curvas das Figuras 4 a 6, que correspondem ao número de casos, à primeira e à segunda derivada, tanto para o número de infectados quanto para o número de mortes, respectivamente.

Figura 4 – Previsão para o número de infectados (a) e o número de mortes (b).

Figura 5 – Previsão para a 1ª derivada do número de casos (a) e número de mortes (b).

Figura 6 – Previsão – 2ª. Derivada do número de casos (a) e número de mortes (b).
Estas curvas nos permitem responder a uma pergunta que incomoda todo o Brasil, quando vai terminar essa pandemia? Uma estimativa seria quando a curva da segunda derivada (Figuras 6.a e 6.b) voltar a atingir a linha do zero, próximo ao 450º dia para o número de pessoas infectadas e próximo de 350º dia para o número de mortes, isso quer dizer que se não ocorrer nada de diferente, tipo a população mudar seu comportamento e aumentar a sua proteção ou se houver uma melhor política de proteção, vamos entrar em 2021 ainda com casos de COVID-19 no Brasil, infelizmente.
O que esperamos é que a população se conscientize e colabore e as políticas públicas de saúde sejam mais assertivas, só assim poderemos modificar esses parâmetros da curva de Gompertz e adiantar o término dessa pandemia que tanto está prejudicando a todos.
Com relação à imunidade de rebanho, existem controvérsias e ainda estamos estudando esse assunto e não temos ainda uma opinião formada. Para quem ainda não sabe esse conceito, imunidade de rebanho é quando já existe uma quantidade suficiente de pessoas infectadas que se recuperaram e o seu organismo criou anticorpos contra o vírus, assim elas desenvolvem uma imunidade e a propagação da doença diminui, não porque o poder de contaminação do agente patogênico tenha diminuído, mas porque diminui a possibilidade de uma pessoa contagiável entrar em contato com uma pessoa infectada. A ideia é que a população imune sirva como barreira que impede que um transmissor da doença o infecte.
Não somos epidemiologistas, somos apenas curiosos. Assim como todo mundo, esperamos que ocorra uma aceleração do decréscimo do número de casos e possamos sair dessa situação o mais rápido possível.
Sabemos que não é uma boa notícia e temos que encarar os fatos. A sugestão que fica é que ainda usemos máscara, lavemos as mãos com frequência, usemos álcool 70º e evitemos aglomerações. Nossos hábitos garantirão nossa saúde!
Referências:
Winsor, C.H. (1931), THE GOMPERTZ CURVE AS A GROWTH CURVE; Proceedings of the National Academy of Sciences, Vol 18, No.1, January 15,1932.
Sobre o Autor:
Edson R. Montoro é Diretor Técnico da ERMontoro Consultoria e Treinamento Ltda, empresa focada no desenvolvimento de pessoas e consultoria nas áreas de melhoria de processo usando Estatística Aplicada e Lean Manufacturing.
O autor é Químico pela UNESP (Universidade Estadual Paulista “Júlio de Mesquita Filho”) – Araraquara, MBA em Gestão Empresarial pela FGV (Fundação Getúlio Vargas), Master Black Belt pela Air Academy Associates, Engenheiro de qualidade pela ASQ (America Society for Quality) e Pós-graduação em Gerência de Produção pela UFSC (Universidade Federal de Santa Catarina).
Comments